2024 MAA AMC 10B
题目1
在一排从左到右排列的人群中,从左数第1013个人同时也是从右数第1010个人。这排共有多少人?(A) 2021 (B) 2022 (C) 2023 (D) 2024 (E) 2025
题目2
\( {10}! - 7! \cdot 6! \) 的值是多少?(A) -120 (B) 0 (C) 120 (D) 600 (E) 720
题目3
对于多少个整数值的 \( x \) , \( \left| {2x}\right| \leq {7\pi } \) 成立?(A) 16 (B) 17 (C) 19 (D) 20 (E) 21
题目4
编号为 \( 1,2,3,\ldots \) 的球按照以下程序被放入5个箱子中,箱子分别标记为A、B、C、D和E。球1被放入箱子A,球2和球3被放入箱子B。接下来的3个球被放入箱子C,再接下来的4个球被放入箱子D,依此类推,在球被放入箱子E后循环回到箱子A。(例如,编号为 \( {22},{23},\ldots ,{28} \) 的球在该过程的第7步被放入箱子B。)球2024被放入哪个箱子?(A) A (B) B (C) C (D) D (E) E
题目5
在以下表达式中,Melanie将一些加号改为减号:\[ 1 + 3 + 5 + 7 + \cdots + {97} + {99}\text{.} \]
当计算新表达式时,结果为负数。Melanie最少需要将多少个加号改为减号?
(A) 14 (B) 15 (C) 16 (D) 17 (E) 18
题目6
一个矩形具有整数边长,面积为2024。该矩形的最小可能周长是多少?(A) 160 (B) 180 (C) 222 (D) 228 (E) 390
题目7
当 \( {7}^{2024} + {7}^{2025} + {7}^{2026} \) 被19除时,余数是多少?(A) 0 (B) 1 (C) 7 (D) 11 (E) 18
题目8
设 \( N \) 为42的所有正整数因子的乘积。 \( N \) 的个位数是多少?(A) 0 (B) 2 (C) 4 (D) 6 (E) 8
题目9
实数 \( a, b \) 和 \( c \) 的算术平均数为0。 \( {a}^{2},{b}^{2} \) 和 \( {c}^{2} \) 的算术平均数为10。那么 \( {ab},{ac} \) 和 \( {bc} \) 的算术平均数是多少?(A) -5 (B) \( - \frac{10}{3} \) (C) \( - \frac{10}{9} \) (D) 0 (E) \( \frac{10}{9} \)
题目10
四边形 \( {ABCD} \) 是平行四边形,且 \( E \) 是边 \( \overline{AD} \) 的中点。设 \( F \) 为直线 \( {EB} \) 与 \( {AC} \) 的交点。求四边形 \( {CDEF} \) 与 \( \bigtriangleup {CFB} \) 的面积之比。(A) 5:4 (B) \( 4 : 3 \) (C) \( 3 : 2 \) (D) \( 5 : 3 \) (E) \( 2 : 1 \)
题目11
下图中 \( {WXYZ} \) 为矩形,且 \( {WX} = 4 \) 和 \( {WZ} = 8 \) 。点 \( M \) 位于 \( \overline{XY} \) 上,点 \( A \) 位于 \( \overline{YZ} \) 上,且 \( \angle {WMA} \) 为直角。三角形 \( \bigtriangleup {WXM} \) 与 \( \bigtriangleup {WAZ} \) 的面积相等。求 \( \bigtriangleup {WMA} \) 的面积?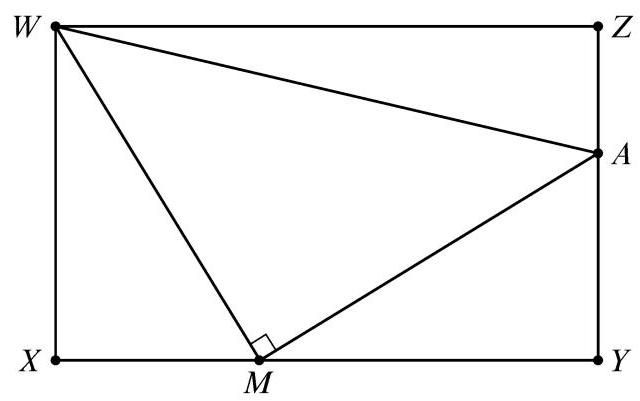
(A) 13 (B) 14 (C) 15 (D) 16 (E) 17
题目12
来自不同国家的100名学生参加数学竞赛。每名学生掌握的语言数量相同,且对于任意两名学生A和B,A掌握一门B不会的语言,B也掌握一门A不会的语言。所有学生掌握的语言总数最少是多少?(A) 9 (B) 10 (C) 12 (D) 51 (E) 100
题目13
正整数 \( x \) 和 \( y \) 满足方程 \( \sqrt{x} + \sqrt{y} = \sqrt{1183} \) 。求 \( x + y \) 的最小可能值。(A) 585 (B) 595 (C) 623 (D) 700 (E) 791
题目14
飞镖靶是坐标平面中的区域 \( B \) ,由满足 \( \left| x\right| + \left| y\right| \leq 8 \) 的点(x, y)组成。目标区域 \( T \) 满足 \( {\left( {x}^{2} + {y}^{2} - {25}\right) }^{2} \leq {49} \) 。飞镖随机落在 \( B \) 内。飞镖落在 \( T \) 内的概率可表示为 \( \frac{m}{n} \cdot \pi \) ,其中 \( m \) 和 \( n \) 为互质的正整数。求 \( m + n \) 。(A) 71 (B) 72 (C) 73 (D) 75 (E) 135
题目15
一个包含9个实数的列表由1、2.2、3.2、6.2、7以及 \( x, y \) 和 \( z \) 组成,且 \( x \leq y \leq z \) 。该列表的极差为7,平均数和中位数均为正整数。有多少个有序三元组(x, y, z)可能?(A) 1 (B) 2 (C) 3 (D) 4 (E) 无穷多个
题目16
杰瑞喜欢玩数字。一天,他把从1到2024的所有整数都写在白板上。然后他反复从白板上选取四个数,擦掉它们,并用它们的和或积替换。(例如,杰瑞的第一步可能是擦掉1、2、3和5,然后写上11,即它们的和,或30,即它们的积。)在反复进行此操作后,杰瑞注意到白板上剩下的所有数都是奇数。此时白板上整数的最大可能数量是多少?题目17
在一场5只蜗牛的比赛中,最多只能出现一次并列,但这次并列可以涉及任意数量的蜗牛。例如,比赛结果可能是:Dazzler第一;Abby、Cyrus和Elroy并列第二;Bruna第五。这场比赛有多少种不同的可能结果?(A) 180 (B) 361 (C) 420 (D) 480 (E) 720
题目18
当一个整数的100次方被125除时,可能有多少种不同的余数?\( \textbf{(A)}1\;\textbf{(B)}2\;\textbf{(C)}5\;\textbf{(D)}{25}\;\textbf{(E)}{125} \)
题目19
在下表中,每个问号应替换为"可能"或"不可能",以表示具有给定斜率的非垂直直线是否可以包含给定数量的格点(坐标均为整数的点)。12个条目中有多少个会是"可能"?| 零 | 恰好一个 | 恰好两个 | 多于两个 | |
| 零斜率 |  |  |  |  |
| 非零有理斜率 |  |  |  |  |
| 无理斜率 |  |  |  |  |
(A) 4 (B) 5 (C) 6 (D) 7 (E) 9
题目20
三双不同的鞋排成一排,要求任意一只左鞋不能与来自不同双的右鞋相邻。这六只鞋共有多少种排法?题目21
两根直管(圆柱体),半径分别为1和 \( \frac{1}{4} \) ,平行地放在水平地面上并相互接触。下图为其正视图。若第三根平行管也放在同一地面上并与这两根管都接触,则其所有可能半径之和为多少?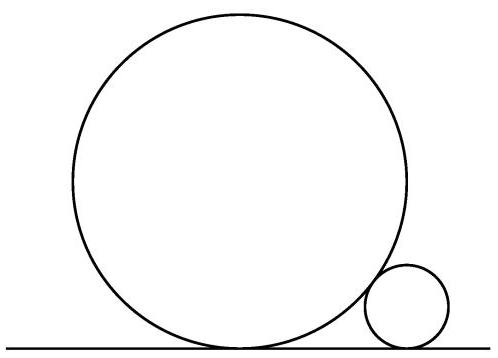
(A) \( \frac{1}{9} \) (B) 1 (C) \( \frac{10}{9} \) (D) \( \frac{11}{9} \) (E) \( \frac{19}{9} \)
题目22
将16人分成4个不可区分的4人委员会。每个委员会设1名主席和1名秘书。这些指派的不同方式总数可写成 \( {3}^{r}M \) ,其中 \( r \) 和 \( M \) 为正整数且 \( M \) 不被3整除。 \( r \) 是多少?(A) 5 (B) 6 (C) 7 (D) 8 (E) 9
题目23
斐波那契数列定义为 \( {F}_{1} = 1,{F}_{2} = 1 \) ,且对 \( n \geq 3 \) 有 \( {F}_{n} = {F}_{n - 1} + {F}_{n - 2} \) 。求\[ \frac{{F}_{2}}{{F}_{1}} + \frac{{F}_{4}}{{F}_{2}} + \frac{{F}_{6}}{{F}_{3}} + \cdots + \frac{{F}_{20}}{{F}_{10}}? \]
(A) 318 (B) 319 (C) 320 (D) 321 (E) 322
题目24
设\[ P\left( m\right) = \frac{m}{2} + \frac{{m}^{2}}{4} + \frac{{m}^{4}}{8} + \frac{{m}^{8}}{8}. \]
在 \( P\left( {2022}\right) , P\left( {2023}\right) , P\left( {2024}\right) \) 和 \( P\left( {2025}\right) \) 这些值中,有多少个是整数?
(A) 0 (B) 1 (C) 2 (D) 3 (E) 4
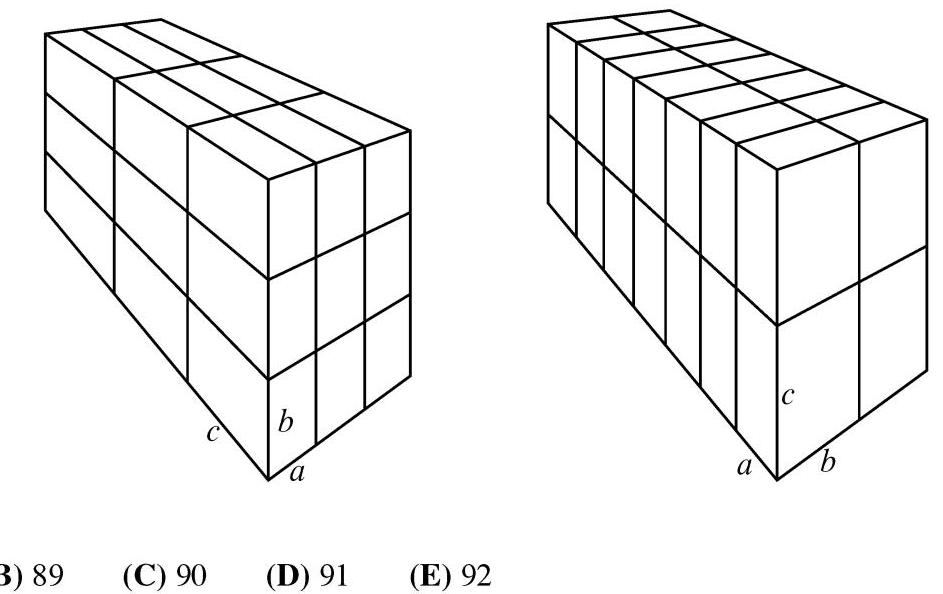
题目25
27块砖(长方体)每块尺寸为 \( a \times b \times c \) ,其中 \( a, b \) 、 \( c \) 为两两互质的正整数。这些砖按左下图所示排成 \( 3 \times 3 \times 3 \) 的长方体。再引入第28块同尺寸砖,并将所有砖重新排成右下图所示的 \( 2 \times 2 \times 7 \) 长方体。新长方体比旧的长、宽、高各增加1个单位。 \( a + b + c \) 是多少?